미국 수학회에서 두 명의 10대 소녀가 피타고라스 정리에 대해 새로운 증명 방법을 프레젠테이션한 것이 화제가 되고 있는데, 응용수학 전문가인 키스 맥널티 씨는 "성별, 민족, 사회인구학적 배경에 관계없이, 기쁨과 열정이 있으면 누구나, 연구 분야에서의 탁월성은 달성 가능하다는 것을 보여주는 훌륭한 사건"이라고 평가하고 있으며, 그 증명 방법 자체가 파문을 일으키고 있다.

American Mathematical Society(미국 수학회, AMS)에 대해서 루이지애나주 뉴올리언스 출신의 10대 소녀인 칼시아 존슨씨와 네키야 잭슨씨의 2명이 프레젠테이션을 실시해, 피타고라스 정리의 새로운 증명을 보여주었다. 두 사람은 학생이며, 아프리카계 미국인 여성이라는 특징은 수학회의 대다수를 차지하는 인구와는 정반대였기 때문에, 맥나르티 씨는 "선택한 연구 분야에서의 탁월성은 누구나 항상 달성 가능하다는 것을 고무하는 훌륭한 사건"이라고 말하고 있다.
또 이 프레젠테이션이 큰 화제를 낳은 데는 큰 이유가 있는데, 증명 방법 자체가 고명한 수학자들을 불러들이는 것이었다고 맥나르티 씨는 전한다.
원래 피타고라스 정리란, "직각 삼각형의 3변의 길이 중, 2변을 알고 있으면 나머지 1변의 길이를 계산할 수 있다"라고 하는 것으로, 「a2+b2=c2」라고 하는 수식으로 나타낸다. 아마 다들 아시다시피...중학교에서 학습하는 수식이지만, 수식의 증명에는 수백 가지나 다른 패턴이 있다.
이 피타고라스 정리의 증명을, "삼각법"을 이용해 한 것이 수학회에 큰 충격을 줬다고 맥나르티 씨는 지적하고 있는데, 삼각법이란, 삼각형 모서리의 크기와 변의 길이의 관계를 기초로 하여, 다른 증명이나 측량 등의 연구에 응용하는 학문 분야인데, 그 삼각법 자체가 피타고라스 정리에 의존하고 있기 때문에, 삼각법으로 피타고라스 정리를 증명하는 것은 "전제 안에 결론을 내린다"는 이른바 순환논법에 해당하므로, "피타고라스 정리를 삼각법으로 증명하는 것은 불가능하다"라고 되어 있었다.
그러나 맥나르티 씨에 따르면, "피타고라스의 정리는 삼각법으로 증명할 수 없다"는 관점은 최근 수십 년간 의문시되는 경우가 많아, 증명이 여러 차례 시도되어 왔다고 하고, 따라서 존슨씨와 잭슨씨의 증명이 "최초의 삼각법에 의한 피타고라스 정리의 증명"인 것은 아니지만, 맥나르티씨는 그들의 증명을 "지금까지 본 것 중 가장 아름답고, 가장 단순한 삼각법의 증명일 가능성이 있습니다"라고 높이 평가하고 있다. 아울러, 이것은 젊고 날카로운 지성이 이룬 일이며, 많은 경험이 풍부한 수학자들의 특징을 명확히 하는 흥미로운 사건이라고 맥나르티 씨는 말한다.
삼각법을 이용한 피타고라스 정리의 새로운 증명에 대해서, 맥나르티씨는 아래의 이미지와 같은 그림으로 나타내고 있는데, 그림에서는 "a-b"라고 가정한 변 a, b, c를 가진 직각삼각형에 대해서, 변 b와 c 사이의 각도를 α, 변 a와 c 사이의 각도를 β라고 하고 있다. 이 직각삼각형에 대해 먼저 "1, 변 b를 축으로 수평 방향으로 반전된 카피를 형성"하고, "2, 변 c에 수직인 직선 A를 각 베타에서 연장"한 후, "3, 직선 A와 변 c를 연결하는 직선 C를 당긴다"라고 하는 3단계를 수행. 그러면 큰 직각삼각형이 형성되고, 그 안에 원래 직각삼각형과 비슷한 직각삼각형을 왼쪽 위에서 점차 작아지는 형태로 무한히 그릴 수 있는데, 이 "무한 상사 삼각형 시퀀스"를 사용하여 직선 A와 C의 길이를 도출하는 것이 존슨 씨와 잭슨 씨의 증명.
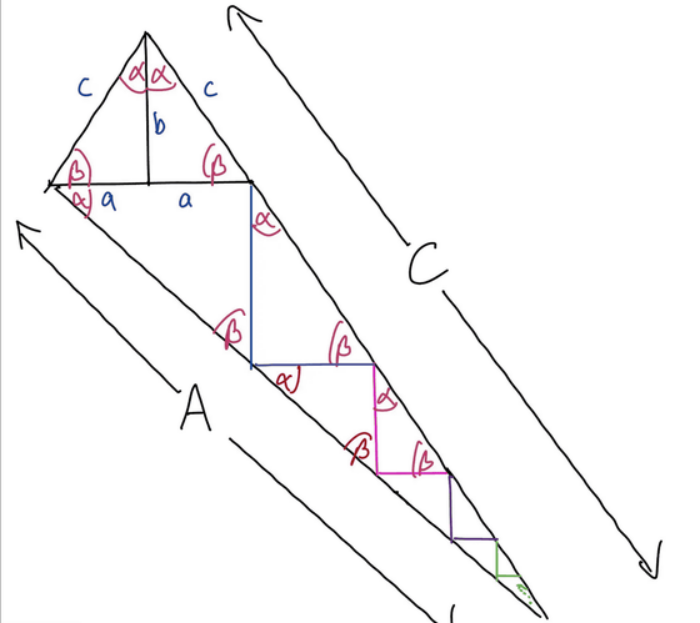
그림에서 볼 수 있듯이, 세 번째 삼각형의 한 변은 2a로 표현되며, "sinα=consβ=a/c", "cosα=sinβ=b/c"라는 삼각비를 이용하면, 그 사변은 "2a/sinβ=2ac/b"로 표현할 수 있다. 이렇게 무한히 이어지는 상사삼각형의 경우에는, 이웃한 삼각형의 변에서 삼각비를 사용해 표현할 수 있고, 이때 상사삼각형 전체 변 A의 길이는 초항 "(2a2c)/b2"·공비 "a2/b2"의 등비급수의 합이 되며, 다음과 같이 나타낼 수 있습니다.
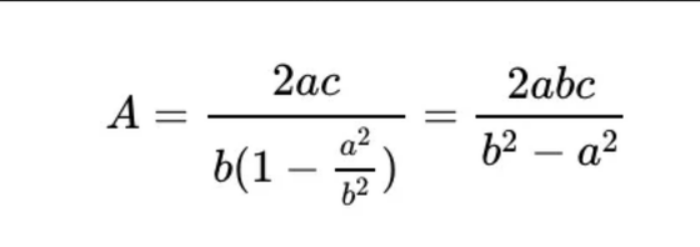
또한 직선 C도 마찬가지로 다음과 같이 나타납니다.

여기서 제시된 A와 C의 비를 계산하면, 다음과 같고 삼각함수에서는 "sinθ=θ의 대변/사변"으로 나타나므로 원래 그림에서 "직선 A/C=sin(2α)"이라고 볼 수 있다.

게다가, 원래 그림의 맨 처음에 직각삼각형을 수평방향으로 복사한 것이고, 두 직각삼각형을 합친 하나의 삼각형은 이등변삼각형으로 되어 있는데, 여기서 증명에 3제곱 정리를 사용하지 않는 정현 정리를 이용하여, 직선 A와 C의 비에 관한 식을 변환했다면 최종적으로 다음과 같은 식이 된다. a,b,c가 모두 0이 아니기 때문에, 분자가 같을 경우에는 분모는 같아질 것이다. 따라서 "a2+b2=c2"로 된다.
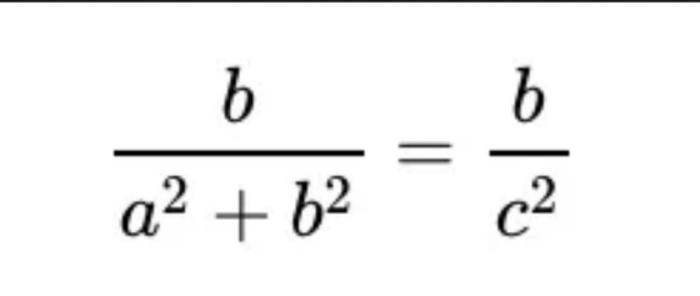
Hacker News에서도 이 증명에 대해 화제가 되고 있으며, "이 증명은 삼각형 변의 비율로서, 사인이나 코사인이 존재한다고 가정하고 있을 뿐, 삼각법을 사용한다는 문구는 오해를 불러일으키는 표현입니다"라고 지적하는 의견이 있는가 하면, "종래에는 사인의 법칙을 증명에 사용할 수 없다는 신념이 있어 피타고라스 정리를 삼각법, 내지 사인이나 코사인을 이용하여 증명하는 것은 불가능하다고 여겨져 왔습니다. 이것이 타파되었기 때문에 창조적이고 예상 밖의 증명이라고 들은 것으로 생각됩니다"라고, 존슨씨와 잭슨씨의 증명 중 무엇이 획기적이었는지를 설명하는 코멘트도 있다는.
또, 수학회에는 별로 유례가 없는 남부 출신 아프리카계 미국인 소녀 2명에 의한 증명이라는 사실이 놀라움을 자아낸 데 대해, 사회적 배경에 의해 학문이 저해되어서는 안 된다는 의견을 포함한 논의가 오가고 있으며, "이들의 증명은 훌륭한 업적임에는 틀림없지만, 맥나르티 씨의 기사에서는 이들이 유명 사립고에 다닌다는 사실을 언급하지 않았습니다. 이 업적에 대해 "학문에 닿기 어려운 영역으로부터의 달성"이라고 하는 스토리를 말하기에는 문제가 있다고 생각합니다"라고 하는 의견도 전해지고 있다.